先来看一个案例：

假设我们有一个不均匀的硬币，有51%的概率正面，49%会反面。选择我们赌注在下一次投掷中，若出现正面，我们盈利相应的bet，反面我们输掉所有的bet。那么，现在有两种策略：
A：投掷一次，赌注1000；
B：投掷1000次，每次赌注1；
你会选A还是B？

因为我们知道硬币是不均匀的，我们有2%的概率优势。现在我们来做一个统计的分析，计算下这两种策略的风险收益比

1.     期望收益：
A： 0.51 * 1000 - 0.49 * 1000 = 20；
B： 1000 （1 * 0.51 - 1 * 0.49） = 20
可见，两种策略有相同的期望收益。

2.      全输概率：
A： 输掉全部资本的概率 = 0.49
B： 输掉全部资本的概率 = 0.49 * 0.49 ... * 0.49  = 0.49^ 1000.

B策略全输的概率远小于A策略

3.   风险评估
A:  stdev(1000,0,0,0 ...0) = 31.6 ；
B：stdev（1，-1,1,1，-1, ... 1) = 1
可见，A策略的标准差远大于A。

4.  夏普比例
A： SR = 20/31.62 = 0.63；
B:  SR = 20/1 = 20

可见，B策略的收益风险比远高于A策略

从这个案例中，我们发现投资核心其实是大数定律。

大数定律即与一个通俗的道理有着莫大的关系。

所谓鸡蛋永远放在一个篮子里，放在投资定理里即是分散投资理论。

在1990年，马科维兹因为“证券投资选择理论”而获得了诺贝尔经济学奖。在其1952年撰写的《证券选择理论》中正是提到了分散投资比集中投资具有更好收益风险比；优秀的投资：要么在同等风险条件下，收益率更高；或者在同样的收益情况下、风险更低。

同时，马科维兹发现，证券投资组合的方差不仅取决于单个资产的方差，而且还取决于各种资产之间的协方差，并且随着组合中证券数目的增加，在决定组合方差时，协方差的作用越来越大，而单个资产方差的作用越来越小，也就是说，协方差几乎成了组合方差的决定性因素！

通过公式我们也可以看出来，当协方差为负数时，是可以减小组合的方差的

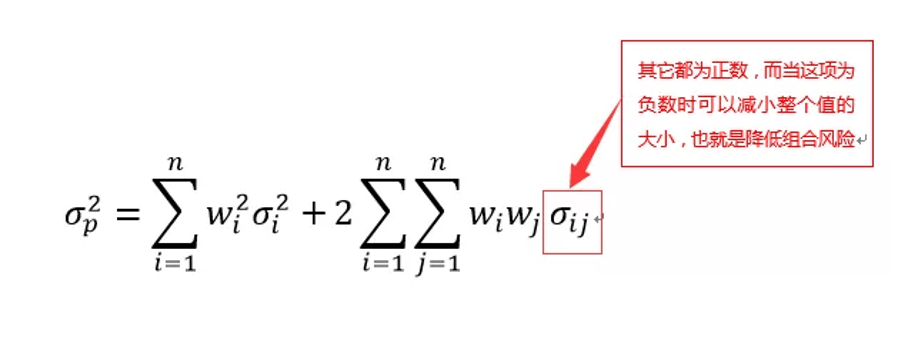
这位诺贝尔经济学奖获得者马科维兹便是将统计学引入金融投资分析的第一人，而其所提出的均值-方差模型也就此开启了量化投资的时代。